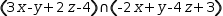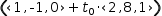9.5 Pseudo-types
A pseudo type imposes a usage or display convention on certain values. It is indicated by a post-fix cast operator (other than one of the formal types) appended to a tuple. Except for certain situations, a pseudo-typed value participates in the type system using its underlying tuple type and representation.
9.5.1 Vectors
An example of an unindicated pseudo type is a convention in which a tuple of scalars or a single-row matrix would be used to represent a vector type. There are several reasons for not doing this but the most important has to do with ambiguities arising from mathematical conventions. In particular, dot product between vectors produces a scalar. While matrix multiplication of single-row matrix with a single-column matrix is a mathematically equivalent operation, it produces a single-element matrix.
9.5.2 Linear Systems
A linear combination is a sum of terms in which each term is a scalar constant or the product of a constant coefficient with a scalar variable. A linear combination incorporated into an equation is called a linear equation.
Linear equations can be represented by individual expressions
but they are commonly gathered into some sort of collection
when related as a system of linear equations.
In Myron, a tuple of linear equations can be parsed
into an augmented matrix of coefficients or produced by deparsing such a matrix.
Both transformations are performed explicitly by the →Linear transformation (see §3.6.6) and implicitly by the solve operator (see §3.7.2).
The linear-system pseudo-type operator ℓ appended to a tuple simply
changes it from a row-like
display to a stacked display. Contrast
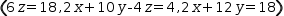
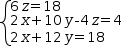
9.5.3 Linear Surfaces
A linear surface is a “flat” shape like a point, a line or a plane defined by a linear combination of vector coefficients with scalar variables. A linear surface can be represented by a tuple of vectors with the convention that the first vector acts as a constant and the other vectors combine with scalar variables in a parametric expression. In conjunction with this convention, functions or transforms can be defined that produce the difference and intersection of linear surfaces. However, all of this is tedious and error-prone and benefits greatly from the introduction of a pseudo-type.
The linear-surface pseudo-type operator “L” interacts with the parser to ensure that its operand is a tuple of vectors. Linear surfaces interact with the display to introduce implied parametric variables and add operators; they interact with intersection and difference operators to perform new linear surfaces; and they can be displayed on the 3-D plotter.
For example, a 3-dimensional plane could be represented by the tuple
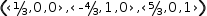
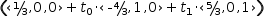
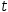
The line of intersection (of it exists) between two planes is obtained from the intersection operator. For example